奇异值分解 Singular Value Decomposition

奇异值分解的定义与性质

定义与定理

$$
A = U\Sigma V^T
$$
A是任意矩阵（$m\times n$），连方阵都不要求。
$U$是正交矩阵orthogonal matrix($m\times m$)，列向量被称为左奇异向量
$V$是正交矩阵orthogonal matrix($n\times n$)，列向量被称为右奇异向量
$\Sigma$是矩形对角矩阵rectangular diagonal matrix($m\times n$)，所有元素非负，且按照降序排列$\Sigma = diag(\sigma_1, \sigma_2,…,\sigma_p)$
$\sigma$为奇异值

奇异值分解定理：任意矩阵A一定存在奇异值分解

紧奇异值分解和截断奇异值分解

$A = U\Sigma V^T$被称为A的完全奇异值分解full SVD, 紧奇异值分解compact SVD是与原始矩阵等秩的奇异值分解；截断奇异值分解truuncate SVD是比原始矩阵低秩的奇异值分解

$A = U\Sigma V^T$为完全奇异值分解
$A = U_r\Sigma_r V_r^T$ 为紧奇异值分解，$U_r$为$U$的前r列，$V_r$为$V$的前r列，$\Sigma_r$为$\Sigma$的前r个对角线元素，$\Sigma_r$的秩与原始矩阵的秩相等。
r为A的秩
$A = U_k\Sigma_k V_k^T$ 为截断奇异值分解，$U_k$为$U$的前k列，$V_k$为$V$的前k列，$\Sigma_k$为$\Sigma$的前k个对角线元素，$\Sigma_k$的秩与原始矩阵的秩相等。
k<r

实际应用中提到奇异值分解一般指截断奇异值分解

几何解释

U是坐标系的旋转或者反射变换，Σ是坐标系的放缩变换，V是坐标系的旋转或者反射变换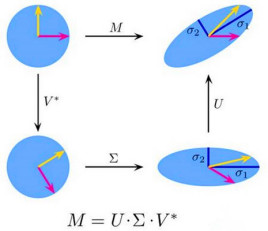在这里插入图片描述

主要性质

（这一部分有些不太懂的，回头再看）

$A^TA$和$AA^T$一定存在特征分解，V的列向量是$A^TA$的特征向量，U的列向量是$AA^T$的特征向量，Σ的奇异值是$A^TA$和$AA^T$特征值的平方根
$$A^Tu_j=\sigma_jv_j\ \ \ \ \ j=1,2,..,n \ A^Tu_j=0 \ \ \ \ \ \ \ j=n+1,n+2,…,m$$
奇异值分解中，Σ是唯一的，U和V不是唯一的
rank(A) = rank($\Sigma$) = # $\sigma_i(\sigma_i>0)$ = r
(没看懂)

奇异值分解的计算

$A^TA$的特征向量为V的列向量；Σ： $A^TA$的特征值开根号，降序排列，放到对角线上，其他地方补0；求正奇异值对应的左奇异值，求扩充的$A^T$的标准正交基，构成U的列。

奇异值分解和矩阵近似

弗罗贝尼乌斯范数Frobenius norm

$$
||A||F=(\sum\limits{i=1}^m\sum\limits_{j=1}^n(a_{ij})^2)^\frac12
$$
（所有元素的平方和开根号）

定理：$||A||_F=||\Sigma||_F=(\sigma_1^2+\sigma_2^2+…+\sigma_n^2)^\frac12$

矩阵的最优近似

奇异值分解是在平方损失（即弗罗贝尼乌斯范数）意义下对矩阵的最优近似，即数据压缩
$rank(A) = r, A=U\Sigma V^T,M$为所有秩不超过k($k\leq r$)的矩阵的集合，一定存在$||A_X||F=\min\limits{S\in M}||A-S||F$，且$||A-X||F=(\sigma{k+1}^2+\sigma{k+2}^2+…+\sigma_n^2)^\frac12$。特别的，当r=k时，$A’=U\Sigma ‘V^T$是达到最优值的矩阵
紧奇异值分解是Frobenius norm意义下的无损压缩
截断奇异值分解是Frobenius norm意义下的有损压缩，k常常远小于r，由于σ递减很快，所以截断奇异值分解也可以有较好的近似

矩阵的外积展开式

$$
U\Sigma = [\sigma_1u_1 \ \ \sigma_2u_2 \ \ \ … \ \ \sigma_nu_n] \
V^T = [v_1^T \ \ \ v_2^T \ \ \ … \ \ \ v_n^T]^T \
A = \sigma_1u_1v_1^T + \sigma_2u_2v_2^T + … + \sigma_nu_nv_n^T \
A_k = \sigma_1u_1v_1^T + \sigma_2u_2v_2^T + … + \sigma_ku_kv_k^T
$$
$A_k$即为A的截断奇异值分解，也是秩为k的最优近似。